Journal & Conference Publications
Click here for compressed view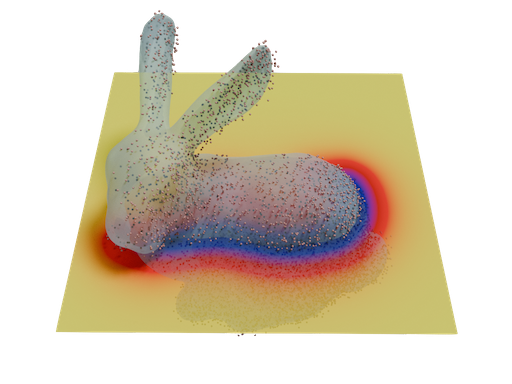
Stochastic Poisson Surface Reconstruction with One Solve using Geometric Gaussian Processes
Mesh Simplification for Unfolding
We propose an algorithm for computationally unfolding 3D shapes isometrically into the plane. Instead of considering this hard problem, we relax the problem and find minimal modifications of the input shape that enable simple unfoldings.

Mirror Bridges Between Probability Measures
We introduce a method to learn a map from a statistical distribution onto itself, allowing us to obtain in-distribution variations of a given input for applications in tasks like generative modeling and others.
Surface-Filling Curve Flows via Implicit Medial Axes
We introduce a fast, robust, and user-controllable algorithm to generate surface-filling curves for interactive design applications. Our geometric flow is orders of mangnitude faster than preivous work, makes minimal assumptions on the input surface and provides tuneable parameters.
Reach for the Arcs:
Reconstructing Surfaces from SDFs via Tangent Points
We introduce an algorithm to reconstruct a mesh from discrete samples of a shape’s Signed Distance Function (SDF). A simple geometric reinterpretation of the SDF lets us formulate the problem through a point cloud, from which a surface can be extracted with existing techniques, outperforming commonly used algorithms and imposing no topological or geometric restrictions.
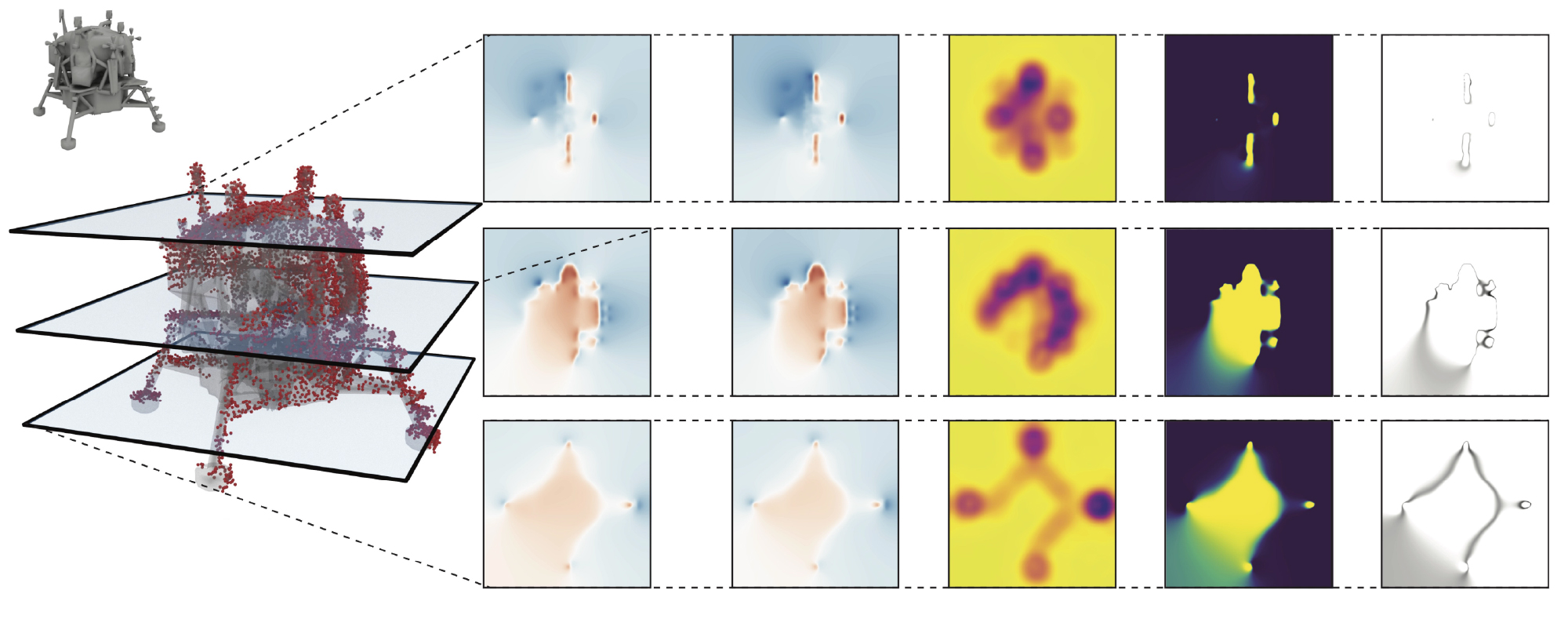
Bayes’ Rays: Uncertainty Quantification for Neural Radiance Fields
We introduce a post-hoc framework to evaluate uncertainty in any pre-trained NeRF without modifying the training process. Our method establishes a volumetric uncertainty field using spatial perturbations and a Bayesian Laplace approximation. We derive our algorithm statistically and highlight its superior performance in key metrics and NeRF-related applications.
Reach for the Spheres:
Tangency-Aware Surface Reconstruction of SDFs
An improved algorithm for isosurfacing of discrete signed distance fields (SDFs) that explicitly interprets each sample point as a sphere to which the surface must lie tangent. Especially at low grid resolutions, it can recover significantly more detail than marching cubes and Neural Dual Contouring.
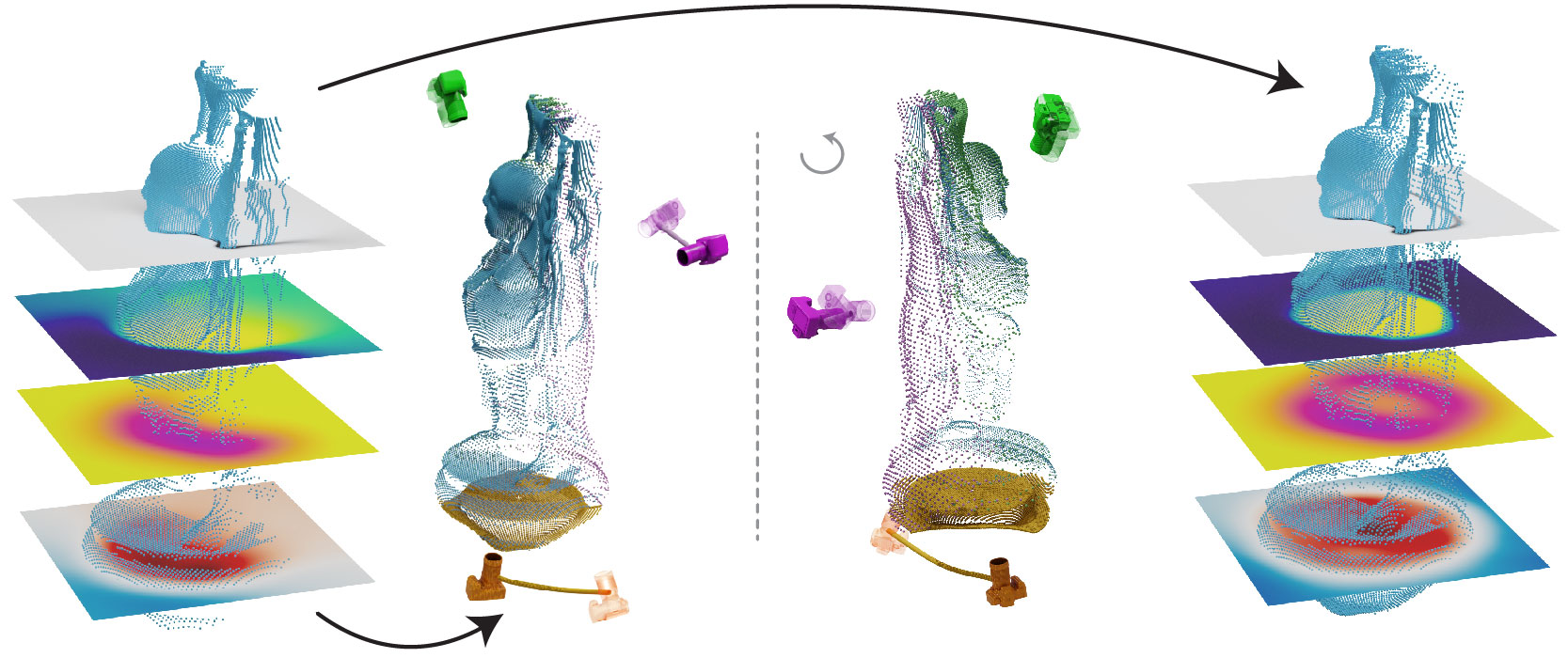
Neural Stochastic Screened Poisson Reconstruction
We use a neural network to study and quantify point cloud surface reconstruction uncertainty under a Poisson smoothness prior. Our algorithm addresses the main limitations of existing work and can be fully integrated into the 3D scanning pipeline, from obtaining an initial reconstruction to deciding on the next best sensor position and updating the reconstruction upon capturing more data.
Constructive Solid Geometry on Neural Signed Distance Fields
We characterize the space of Pseudo-SDFs, which are eikonal yet not true distance functions, and derive a novel regularizer that encourages the output to be an exact SDF. We demonstrate the applicability of our regularization to many operations in which traditional methods cause a Pseudo-SDF to arise, such as CSG and swept volumes, and produce a true (neural) SDF for the result of these operations.
Stochastic Poisson Surface Reconstruction
We introduce a statistical extension of the classic Poisson Surface Reconstruction algorithm for recovering shapes from 3D point clouds. Instead of outputting an implicit function, we represent the reconstructed shape as a modified Gaussian Process. This perspective improves PSR’s integration into the online scanning process, broadens its application realm, and opens the door to other lines of research such as applying task-specific priors.
Breaking Bad: A Dataset for Geometric Fracture and Reassembly
We introduce a large-scale dataset of fractured objects, which serves as a benchmark that enables the study of fractured object reassembly and presents new challenges for geometric shape understanding.
Breaking Good: Fracture Modes for Realtime Destruction
Drawing a direct analogy with the well-studied vibration or elastic modes, we introduce an object’s fracture modes, which constitute its preferred or most natural ways of breaking. Any realtime impact can be projected onto our modes to obtain impact-dependent fracture patterns without the need for any online crack propagation simulation.
Sex and Gender in the Computer Graphics Research Literature
We survey the treatment of sex and gender in the Computer Graphics research literature from an algorithmic fairness perspective. We conclude current trends on the use of gender in our research community are scientifically incorrect and constitute a form of algorithmic bias with potential harmful effects. We propose ways of addressing these trends as technical limitations.
Swept Volumes via Spacetime Numerical Continuation
We propose a novel method to compute the region of space covered by an object as it moves along a trajectory. Compared to other methods, our approach is not restricted to a limited class of shapes or trajectories, is extremely robust, and its asymptotic complexity is an order lower than standards used in the industry, enabling its use in applications such as modeling, constructive solid geometry, and path planning.
Opening and Closing Surfaces
We propose a new type of curvature flow inspired by the mathematical morphology opening and closing operations. Our surface-only curvature-based flow moves the surface selectively in areas that should be repositioned. In our triangle mesh discretization, vertices in regions unaffected by the opening or closing will remain exactly in place and do not affect our method’s complexity, which is output-sensitive.
Developability of Heightfields via Rank Minimization
We propose an algorithm to approximate heightfield surfaces with piecewise-developable (isometric to the plane) patches. Our algorithm builds on our observation that developability can be phrased as a minimal rank constraint on the heightfield’s Hessian, leading to a convex optimization problem.
Solid Geometry Processing on Deconstructed Domains
Rather than create a single volumetric mesh for an entire shape, we advocate for solid geometry processing on the overlapping solid subdomains that compose it combined with algebraic coupling. We demonstrate the superiority of this method through empirical convergence tests and qualitative applications to solid geometry processing on a variety of popular second-order and fourth-order partial differential equations.